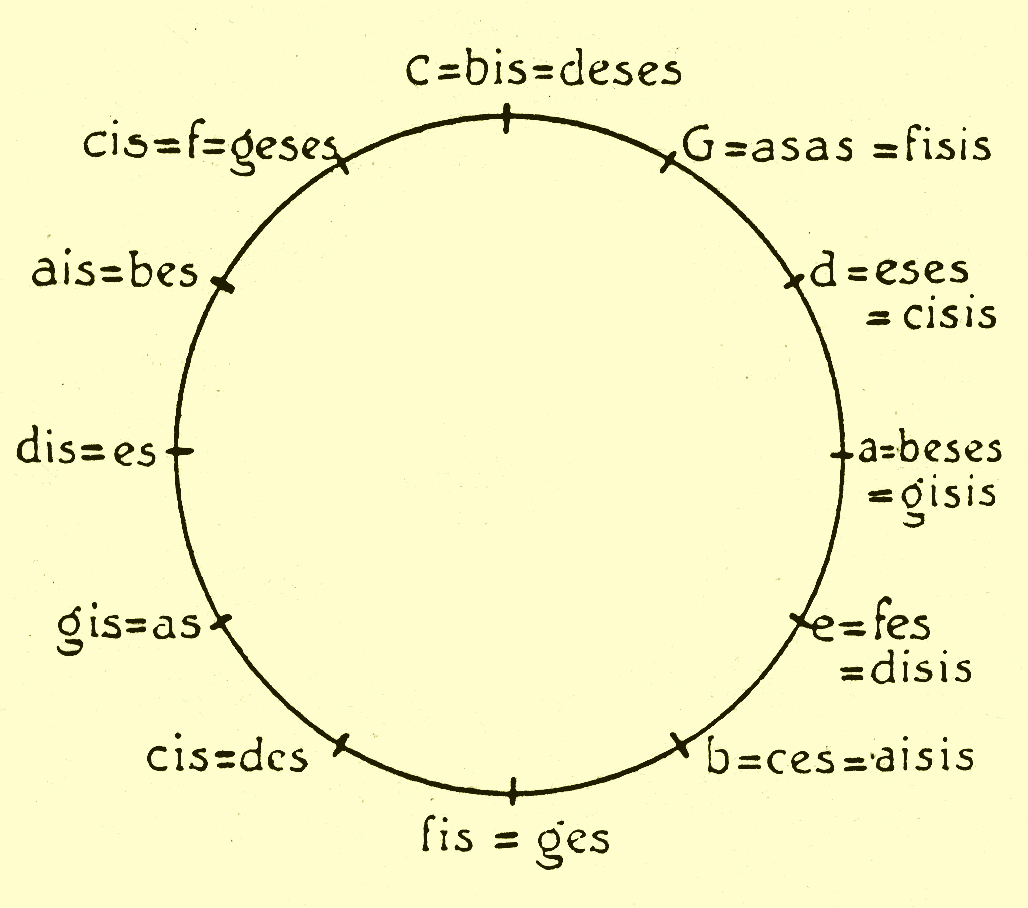
De kwintenspiraal
Met behulp van het monochord hebben we al eerder de tonen van de diatonische toonladder gevonden. Deze tonen (a-b-c-d-e-f-g) noemen we de stamtonen. We gaan het aantal tonen verder uitbreiden door dezelfde berekeningen toe te passen. Vanaf b’ gaan we steeds een kwint omhoog, maar om in het eengestreept octaaf te blijven, gaan we af en toe een octaaf omlaag.
De uitgerekende toon krijgt dezelfde naam als de stamtoon die daar onder ligt, met de toevoeging van een kruis (notennaam + toevoeging is).
van b’ naar fis’: 3/4 x 495,000Hz =371,250Hz (=kwint omhoog, oktaaf omlaag)
van fis’ naar cis’: 3/4 x 371,250Hz =278,4375Hz (=kwint omhoog, oktaaf omlaag)
van cis’ naar gis’: 3/2 x 278,4375Hz =417,656Hz (=alleen kwint omhoog)
van gis’ naar dis’: 3/4 x 417,656Hz =313,242Hz (=kwint omhoog, oktaaf omlaag)
van dis’ naar ais’: 3/2 x 313,242Hz =469,863Hz (=alleen kwint omhoog)
Als we de toonhoogtes van deze tonen op het grafiekpapier met logaritmische indeling zetten (waar we al eerder de diatonische toonladder op hebben genoteerd), dan zien we dat deze tonen een halve toon hoger liggen dan de stamtonen. De toonladder is nu opgedeeld in twaalf halve toonsafstanden.
We gaan nog een paar stappen verder.
van ais’ naar eis’: 3/4 x 469,863Hz =352,397Hz (=kwint omhoog, oktaaf omlaag)
van eis’ naar bis’: 3/2 x 352,397Hz =528,596Hz (=alleen kwint omhoog)
Uit de berekeningen is te zien dat de toonhoogte van eis’ vlakbij de toonhoogte van f ’ ligt en dat de toonhoogte van bis’ vlakbij de toonhoogte van c’’ ligt.
Dit betekent: eis’ is enharmonisch gelijk aan f ’ en bis’ is enharmonisch gelijk aan c’’ .
Nu gaan we vanaf f ’ steeds een kwint omlaag, maar om in het eengestreept octaaf te blijven, gaan we af en toe een octaaf omhoog.
De uitgerekende toon krijgt dezelfde naam als de stamtoon die daar boven ligt, met de toevoeging van een mol (notennaam + toevoeging es of s).
van f’ naar bes’: 4/3 x 347,654Hz =463,5387Hz (=kwint omlaag, oktaaf omhoog)
van bes’ naar es’: 2/3 x 463,5387Hz =309,0258Hz (=alleen kwint omlaag)
van es’ naar as’: 4/3 x 309,0258Hz =412,0344Hz (=kwint omlaag, oktaaf omhoog)
van as’ naar des’: 2/3 x 412,0344Hz =274,690Hz (=alleen kwint omlaag)
van des’ naar ges’: 4/3 x 274,690Hz =366,2528Hz (=kwint omlaag, oktaaf omhoog)
Als we de toonhoogtes van deze tonen op het grafiekpapier zetten, dan zien we dat ze een halve toon lager liggen ten opzichte van de stamtonen. en dat ze vlakbij de verhoogde tonen liggen. Dit betekent: bes’ is enharmonisch gelijk aan ais’, es’ is enharmonisch gelijk aan dis’, as’ is enharmonisch gelijk aan gis’, des’ is enharmonisch gelijk aan cis’, en ges’ is enharmonisch gelijk aan fis’ .
We gaan ook nu nog een paar stappen verder.
van ges’ naar ces’’: 4/3 x366,2528Hz =488,337Hz (=kwint omlaag, oktaaf omhoog)
van ces’ naar fes’: 3/2 x 488,337Hz =325,558Hz (=alleen kwint omlaag)
Uit de berekeningen is te zien dat de toonhoogte van ces’’ vlakbij de toonhoogte van b’ ligt en dat de toonhoogte van fes’ vlakbij de toonhoogte van e’ ligt.
Dit betekent: ces’’ is enharmonisch gelijk aan b’ en fes’ is enharmonisch gelijk aan e’ .
De zojuist verkregen toonladder heet chromatische toonladder. Naast de stamtonen worden in stijgende richting de kruisen en in dalende richting de mollen gebruikt.
Extra informatie:
De reine kwinten van het Pythagoreïsche stelsel kunnen we ons voorstellen als een spiraal die is verdeeld in 12 gelijke stukken.
Elk stuk is de voorstelling van een reine kwint.
Zo heeft elke toon uit de chromatische toonladder zijn eigen plek.
Om op hetzelfde punt uit te komen gaan we 12 kwinten omhoog en 7 oktaven omlaag. Dit levert de formule (3:2)^12:2^7 op, wat als uitkomst geeft de verhouding 531441:524288 = 1,013643265:1.
Dit wordt de komma van Pythagoras genoemd, wat neerkomt op 23,46 cents. Dit verschil in toonhoogte is duidelijk hoorbaar.
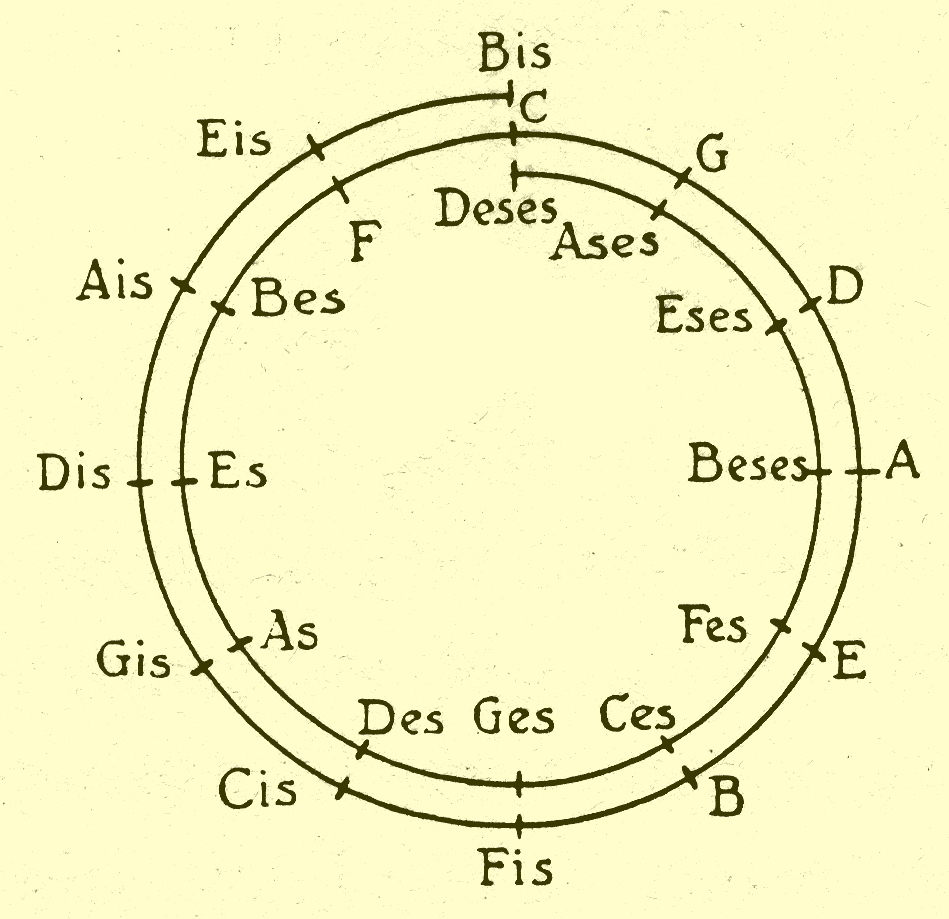
De gesloten kwintencirkel
Om na de twaalf kwinten het octaaf toch rein te laten worden, zal ergens in die 12 kwinten een verkleining moeten worden toegepast.
Door dit compromis wordt de kwintenspiraal omgezet in een kwintencirkel.
De terts
In het stelsel van Pythagoras wordt geen geen gebruik gemaakt van het monochord om andere belangrijk intervallen binnen het octaaf te vinden,
zoals de reine grote en kleine terts.
Het was met name Ptolemaeus, een astronoom en wiskundige in Alexandrië (80 - 150 n. Chr.)
die de onzuivere Pythagoreïsche tertsen verving door reine tertsen, gevonden met behulp van het monochord.
In zijn boek 'Harmonicorum libri tres' (bekend door de vertaling door Wallis, 1699) geeft hij een aantal eigen voorstellen.
De bekendste hiervan heet het Diatonisch Syntonon of wel de Reeks van Ptolemaeus:
e - 10/9 - d - 9/8 - c - 16/15 - b - 9/8 - a - 10/9 - g - 9/8 - f 16/15 - e
Uit deze reeks van secundes kunnen we de andere intervallen halen. De reine grote terts: 9/8 x 10/9 = 4/5 en de reine kleine terts: 9/8 x 16/15 = 6/5 .
We kunnen ook zien dat de Reeks van Ptolemaeus alleen de priemgetallen 2, 3, en 5 bevat (vgl. tweede, derde en vijfde harmonsiche).
De muziektheoretici van de 16e en de 17e eeuw (die zich graag beriepen op klassieke voorbeelden) gaven vooral aan de stemmingen van Didymos
en de stemming volgens het Diatonisch Syntonon de voorkeur vanwege hun reine tertsen.
De methode om het compromis tussen kwintencirkel en octaaf te sluiten, heeft in de loop der eeuwen aanleiding gegeven tot een zeer groot aantal variaties in stemmingen.
Al deze stemmingen leveren een compromis op, waarbij bepaalde intervallen of minder mooi worden of geheel onspeelbaar zijn (de zogenaamde wolven vanwege de associatie met wolfsgehuil).